Matrices and their Eigenvalues

back to home page

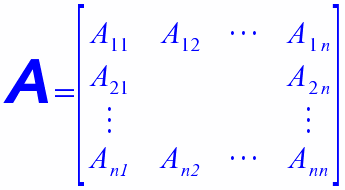
Matrices are widely used in maths, physics and other sciences to represent linear relations between many 'inputs' and many 'outputs'. The matrix is an array of elements, a_ij, each of which gives the weight of the jth input in its effect on the ith output. In maths text books they appear in 'linear algebra'. Here I deal only with square matrices, which are ones with the same number of rows as there are columns.

A matrix can be pictured as operating (by matrix multiplication) on a set of input values (written in the form of a vector) to convert it into set of outputs (also written in the form of a vector). Geometrically this corresponds to the matrix stretching and rotating the input vector into the output one. An N-by-N square matrx can be thought of as operating in an N-dimensional space. Each N by N matrix has a set of N special directions in that space which have the distinguishing property that they are not rotated by the matrix multiplication operation. In general the input vector along each one of these directions is stretched or shrunk or swapped in the sense it points, but not otherwise rotated. These are the 'eigenvectors' and the scaling stretch factors are the 'eigenvalues'. These words come from the German language and mean 'characteristic' or 'own' since they effectively characterise the action of the matrix.

I have written two articles on matrices and their eigenvalues. One is about numerical methods for finding the eigenvalues and eigenvectors, especially for quite large matrices. The second is about the statistical properties of the eigenvalues of matrices whose elements are random numbers. Both are large fields of study. Indeed, random matrices have been shown to model seemingly unrelated situations in maths and physics, including the distribution of complex zeros of the Riemann zeta function and the energy levels of heavy atomic nuclei.

Article 1: "Iterative numerical methods for real eigenvalues and eigenvectors of matrices"